Question

Direct mail advertisers send solicitations​ ("junk mail") to thousands of potential customers in the hope that some will buy the​ company's product. The response rate is usually quite low. Suppose a company wants to test the response to a new flyer and sends it to 1140 people randomly selected from their mailing list of over​ 200,000 people. They get orders from 122 of the recipients. Use this information to complete parts a through d.Create a 95% confidence interval for the percentage of people the company contacts who may buy something. (Show your work. Step by step)

Answer 1

Answer: (0.089, 0.125)

Explanation:

Confidence interval for population proportion is given by :-

`\hat{p}\pm z^*\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

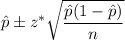
, where n= sample size.

`\hat{p}` = Sample proportion.

z*= Critical z-value.

Let p be the population proportion of people the company contacts who may buy something.

As per given , sample size : n= 1140

Number of recipients ordered = 122

Then,
`\hat{p}=(122)/(1140)\approx0.107`

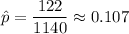
Critical value for 95% confidence interval = z*= 1.96 (By z-table)

So , the 95% confidence interval for the percentage of people the company contacts who may buy something:

`0.107\pm (1.96)\sqrt{(0.107(1-0.107))/(1140)}`

`=0.107\pm (1.96)√(0.000083817)`

`=0.107\pm (1.96)(0.00915516)`

`=0.107\pm 0.018`

`=(0.107-0.018,\ 0.107+0.018)=(0.089,\ 0.125)`

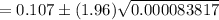
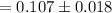
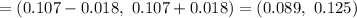
Hence, the 95% confidence interval for the percentage of people the company contacts who may buy something = (0.089, 0.125)