Question

A model for a​ company's revenue from selling a software package is ​R(p)equals=−2.52^2400​p, where p is the price in dollars of the software. What price will maximize​ revenue? Find the maximum revenue.

Answer 1

A model for a​ company's revenue from selling a software package is ​R(p)=-2.5p² + 400​p, where p is the price in dollars of the software. What price will maximize​ revenue? Find the maximum revenue.

Answer: p = $80, R = $16,000

Explanation:

The maximum is the y-value of the Vertex.

Step 1: Use the Axis-Of-Symmetry (AOS) formula to find x:

x=
`(-b)/(2a)`

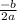
R(p) = -2.5p² + 400

a= -2.5 b=400

`p=(-(400))/(2(-2.5))`

=
`(-400)/(-5)`

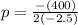
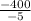
=80

∴ In order to maximize the value, the company will sell the software package for $80

Step 2: Find the maximum by plugging the p-value (above) into the given equation.

R(80) = -2.5(80)² + 400(80)

= -16,000 + 32,000

= 16,000