Question

Evaluate the integral Integral from nothing to nothing ∫ StartFraction 3 Over t Superscript 4 EndFraction 3 t4 sine left parenthesis StartFraction 1 Over t cubed EndFraction minus 6 right parenthesis sin 1 t3 −6dt

Answer 1

`\cos ((1)/(t^3)-6)} + c`

Explanation:

Given function:

`\int {(3)/(t^4)\sin ((1)/(t^3)-6)} \, dt`

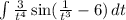
Now,

let
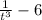`(1)/(t^3)-6` be 'x'

Therefore,

`d((1)/(t^3)-6)` = dx

or

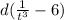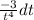`(-3)/(t^4)dt` = dx

on substituting the above values in the equation, we get

⇒ ∫ - sin (x) . dx

or

⇒ cos (x) + c [ ∵ ∫sin (x) . dx = - cos (x)]

Here,

c is the integral constant

on substituting the value of 'x' in the equation, we get

`\cos ((1)/(t^3)-6)} + c`