Question

Anyone good in LAW OF SINES??​

Answer 1

Explanation:

Answer 2

b = 6.7cm

Explanation:

The law of sines is:

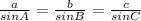`(a)/(sinA) =(b)/(sinB) =(c)/(sinC)` OR
`(sinA)/(a) =(sinB)/(b) =(sinC)/(c)`

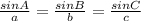
Each section represents an angle (capital) and its opposite side (lowercase). When you use it, only use two sections at a time. You may have one missing piece of information when using it. Use the formula that puts the missing information in the numerator (top).

This problem:

We are given one set of information, 8cm and 55°. This can be "a" and "A" (not labelled).

We need angle B to find side b.

Since we are given two of the three angles in the triangle, and the sum of all interior angles of any triangle is 180°, we can find the missing angle.

∠B = 180° - (∠A + ∠C)

∠B = 180° - (55° + 82°)

∠B = 43°

Use the law of sines with sections "A" and "B", with the lowercase letters in the top.

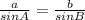`(a)/(sinA) =(b)/(sinB)` Substitute known measurements

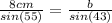`(8cm)/(sin(55)) =(b)/(sin(43))` Rearrange to isolate "b"

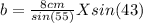`b = (8cm)/(sin(55))X{sin(43)}` Solve, degree mode on calculator

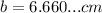`b = 6.660...cm` Exact answer

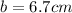`b = 6.7cm` Rounded to nearest tenth

Therefore side b is 6.7cm.