Answer:
a)
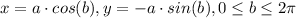
b)
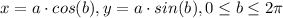
c)
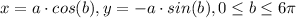
d)
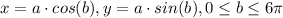
Step-by-step explanation:
The parametric equation for a circle is:
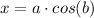
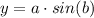
Where a is the radius and b is the angular displacement.
a) If a is negative in y and 0 ≤ b ≤ 2π, we have clockwise moves.
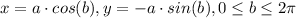
b) If a is positive in y and 0 ≤ b ≤ 2π, we have counterclockwise moves.
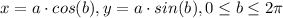
c) If a is negative in y and 0 ≤ b ≤ 6π, we have three times clockwise moves.
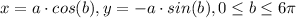
d) If a is positive in y and 0 ≤ b ≤ 6π, we have three times counterclockwise moves.
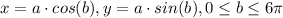
Have a nice day!