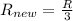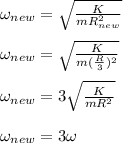Question

Would the frequency of the angular simple harmonic motion (SHM) of the balance wheel increase or decrease if the dimensions of the balance wheel were changed as described?

Answer 1

Yes the frequency of the angular simple harmonic motion (SHM) of the balance wheel increases three times if the dimensions of the balance wheel reduced to one-third of original dimensions.

Step-by-step explanation:

Considering the complete question attached in figure below.

Time period for balance wheel is:

`T=2\pi\sqrt{(I)/(K)}`

`I=mR^(2)`

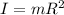
m = mass of balance wheel

R = radius of balance wheel.

Angular frequency is related to Time period as:

`\omega=(2\pi)/(T)\\\omega=\sqrt{(K)/(I)} \\\omega=\sqrt{(K)/(mR^(2))`

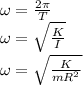
As dimensions of new balance wheel are one-third of their original values

`R_(new)=(R)/(3)`

`\omega_(new)=\sqrt{(K)/(mR_(new)^(2))}\\\\\omega_(new)=\sqrt{(K)/(m((R)/(3))^(2))}\\\\\omega_(new)={3}\sqrt{(K)/(mR^(2))}\\\\\omega_(new)={3}\omega`