Question

The height of a cone is increasing at a rate of 10 cm/sec and its radius is decreasing so that its volume remains constant. How fast is the radius changing when the radius is 4 cm and the height is 10 cm?

Answer 1

dr/dt = -2 cm/s.

Step-by-step explanation:

The volume of a cone is given by:

`V=(1)/(3) \pi r^(2)h` (1)

• r is the radius
• h is the height

Let's take the derivative with respect to time in each side of (1).

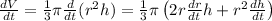`(dV)/(dt)=(1)/(3) \pi (d)/(dt)(r^(2)h)=(1)/(3) \pi \left(2r(dr)/(dt)h+r^(2)(dh)/(dt) \right)` (2)

We know that:

• dh/dt = 10 cm / s (rate increasing of height)
• dV/dt = 0 (constant volume means no variation with respect of time)
• r = 4 cm
• h = 10 cm

We can calculate how fast is the radius changing using the above information.

`0=(1)/(3) \pi \left( 2\cdot 4\cdot (dr)/(dt) \cdot 10 + 4^(2)\cdot 10)\right`

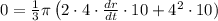
Therefore dr/dt will be:

`(dr)/(dt)=-(160)/(80)=-2 cm/s`

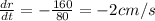
The minus signs means that r is decreasing.

I hope it helps you!