Question

Howdy! Id love to have these questions answered asap! Thank you for the help!

1) Which angle is not coterminal to 120 degrees?
A. 840
B. -180
C. 480

2) Use the unit circle and the reference angle to determine which of the following trigonometric values is correct when theta = -90
A. Cos theta = undefined
B. Sin theta = -1
C. Tan = 0

Answer 1

1) Which angle is not coterminal to 120 degrees?

A. 840

B. -180

C. 480

Answer:

From given options, -180 is not a coterminal angle of 120 degrees

Solution:

Coterminal Angles are angles who share the same initial side and terminal sides.

Finding coterminal angles is as simple as adding or subtracting 360° or 2π to each angle, depending on whether the given angle is in degrees or radians

Coterminal angles of 120 degrees are:

120 degrees + 360 degrees = 480 degrees

120 degrees - 360 degrees = 240 degrees

720 degrees + 120 degrees = 840 degrees

120 degrees - 720 degrees = -600 degrees

Therefore:

Positive Angle 1 (Degrees) 480

Positive Angle 2 (Degrees) 840

Negative Angle 1 (Degrees) -240

Negative Angle 2 (Degrees) -600

Therefore from given options, -180 is not a coterminal angle of 120 degrees

2) Use the unit circle and the reference angle to determine which of the following trigonometric values is correct when theta = -90

A. Cos theta = undefined

B. Sin theta = -1

C. Tan theta = 0

Answer:

Sin theta = -1 is correct

Solution:

given angle is -90

Find the reference angle for -90

Reference angle = 360 - 90 = 270 degrees

Unit circle diagram is attached below

And from the unit circle, we know the coordinates for 270 degrees are (0, -1)

Our angle - 90 degrees lies in (0, -1)

Unit circle coordinates are given by
`(cos \theta , sin \theta )`

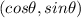
This means,

cos (-90 ) = 0 and sin(-90) = -1

We know that,

`tan \theta = (sin \theta)/(cos \theta)`

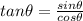
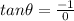`tan \theta = (-1)/(0)` = undefined

Therefore from options, sin theta = -1 is correct