Question

Suppose that a random sample of size 49 is to be selected from a population with mean 49 and standard deviation 6. What is the approximate probability that Xwll be more than 0.5 away from the population mean?

a 0.4403
b) 0.6403
c) 0.8807
d) 0.0664
e) 0.5597
f) None of the above

Answer 1

Option e - 0.5597

Explanation:

Given : Suppose that a random sample of size 49 is to be selected from a population with mean 49 and standard deviation 6.

To find : What is the approximate probability that will be more than 0.5 away from the population mean?

Solution :

Applying z-score formula,

`z=(x-\mu)/((\sigma)/(√(n)))`

Here,
`\mu=49,\sigma=6, n=49`

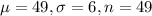
As, probability that will be more than 0.5 away from the population mean

i.e. x=49.5,

`z=(49.5-49)/((6)/(√(49)))`

`z=(0.5)/(0.857)`

`z=0.58`

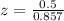
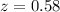
In z-score table the value of z at 0.58 is 0.7190.

x=48.5,

`z=(48.5-49)/((6)/(√(49)))`

`z=(-0.5)/(0.857)`

`z=-0.58`

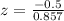
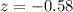
In z-score table the value of z at -0.58 is 0.2810.

Now, probability that will be more than 0.5 away from the population mean is given by,

`P=P(X>49.5)+P(X<48.5)`

`P=1-P(X<49.5)+P(X<48.5)`

`P=1-0.7190+0.2810`

`P=0.562`

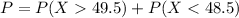
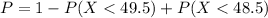
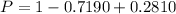
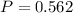
Therefore, option e is correct.