Question

Wire resistor A has twice the length and twice the cross sectional area of wire resistor B. Which of the following accurately compares the resistances of wire resistors A and B?a) Wire A has twice the resistance of wire B.b) Wire A has half the resistance of wire B.c) Wire A has the same resistance as wire B.d) None of the above

Answer 1

Answer: Option (c) is the correct answer.

Step-by-step explanation:

It is known that the relation between resistance, length and cross-sectional area is as follows.

R =
`\rho (l)/(A)`

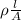
Let the resistance of resistor A is denoted by R and the resistance of resistor B is denoted by R'.

Hence, for resistor A the expression for resistance according to the given data is as follows.

R =
`\rho (2l)/(2A)`

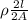
On cancelling the common terms we get the expression as follows.

R =
`\rho (l)/(A)`

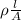
Now, the resistance for resistor B is as follows.

R' =
`\rho (l')/(A')`

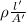
Thus, we can conclude that the statement, Wire A has the same resistance as wire B, accurately compares the resistances of wire resistors A and B.