Answer:
Option B is the required answer.
Explanation:
As per the given question,
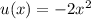 and
and
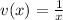 .
.
Hence, (u circle v) (x) = u{v(x)} =
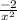
The range of the function, (u circle v) (x) means the set of the values of x so that we will be able to get a proper finite, countable and exact value of the function.
For the above function, (u circle v) (x) we can not get a proper value of the function for x = 0.
Hence, the options A, C, D can not be the range of the function, since it contains 0.
The range of the given function will be the option B, since it does not contain the value 0.