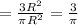Question

A square and a circle intersect so that each side of the square contains a chord of the circle equal in length to the radius of the circle. What is the ratio of the area of the square to the area of the circle? Express your answer as a common fractin in terms of Pie.

Answer 1

Explanation:

it is given that Square contains a chord of of the circle equal to the radius thus from diagram

`QR=chord =radius =R`

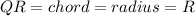
If Chord is equal to radius then triangle PQR is an equilateral Triangle

Thus
`QO=(R)/(2)=RO`

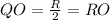
In triangle PQO applying Pythagoras theorem

`(PQ)^2=(PO)^2+(QO)^2`

`PO=√((PQ)^2-(QO)^2)`

`PO=\sqrt{R^2-(R^2)/(4)}`

`PO=(√(3))/(2)R`

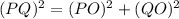
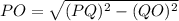
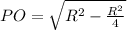
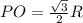
Thus length of Side of square
`=2PO=√(3)R`

Area of square
`=(√(3)R)^2=3R^2`

Area of Circle
`=\pi R^2`

Ratio of square to the circle
`=(3R^2)/(\pi R^2)=(3)/(\pi )`