Question

Suppose you solved a second-order equation by rewriting it as a system and found two scalar solutions: y = e^5x and z = e^2x. Think of the corresponding vector solutions y1 and y2 and use the Wronskian to show that the solutions are linearly independent Wronskian = det [ ] = These solutions are linearly independent because the Wronskian is [ ] Choose for all x.

Answer 1

The solutions are linearly independent because the Wronskian is not equal to 0 for all x.

The value of the Wronskian is
`\bold{W=-3e^(7x)}`

Explanation:

We can calculate the Wronskian using the fundamental solutions that we are provided and their corresponding the derivatives, since the Wroskian is defined as the following determinant.

`W = \left|\begin{array}{cc}y&z\\y'&z'\end{array}\right|`

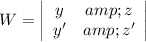
Thus replacing the functions of the exercise we get:

`W = \left|\begin{array}{cc}e^(5x)&e^(2x)\\5e^(5x)&2e^(2x)\end{array}\right|`

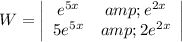
Working with the determinant we get

`W = 2e^(7x)-5e^(7x)\\W=-3e^(7x)`

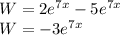
Thus we have found that the Wronskian is not 0, so the solutions are linearly independent.