Question

25. Algebraically determine whether the function k(x) = x6 - x2 + 7 is odd, even, or neither. Explain your

reasoning

Answer 1

Answer: The function is EVEN.

Explanation:

For this exercise it is important to remember that:

1. A function f(x) is even if and only if:

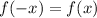`f(-x) = f(x)` for all "x"

2. A function f(x) is odd if and only if:

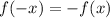`f(-x) = -f(x)` for all "x"

So knowing that, and given the following function k(x):

`k(x)=x^6 - x^2 + 7`

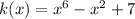
You can plug
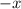`-x` in for "x", order to know if this is even. Then, you get:

`k(-x)=(-x)^6 - (-x)^2 + 7\\\\k(-x)=x^6-x^2+7`

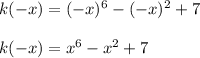
Therefore, since:

`f(-x) = f(x)`

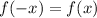
You can determine that that the given function
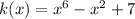`k(x)=x^6 - x^2 + 7` is Even.