Question

4. You want to know if there's an association between college students' spring break destinations and what year they're in. You take a random sample of 405 college students and record the following data: Amusement Parks Mexico Home Other Freshman 23 21 43 21 Sophomore 34 23 14 26 Junior 25 30 23 26 Senior 27 33 17 19 A. Set up your null and alternative hypotheses. (2 points)

Answer 1

`\chi^2 =27.356`

`p_v = P(\chi^2_(9) >27.356)=0.00122`

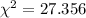
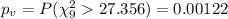
And we can find the p value using the following excel code:

"=1-CHISQ.DIST(27.356,9,TRUE)"

Since the p value is lower than the significance level assumed 0.05 we can reject the null hypothesis at 5% of significance, and we can conclude that we have association between the two variables analyzed.

Explanation:

A chi-square goodness of fit test "determines if a sample data matches a population".

A chi-square test for independence "compares two variables in a contingency table to see if they are related. In a more general sense, it tests to see whether distributions of categorical variables differ from each another".

Assume the following dataset:

Amusement Parks Mexico Home Other Total

Freshman 23 21 43 21 108

Sophomore 34 23 14 26 97

Junior 25 30 23 26 104

Senior 27 33 17 19 96

Total 109 107 97 92 405

We need to conduct a chi square test in order to check the following hypothesis:

H0: There is independence between the two random variables

H1: There is dependence between the two variables

The level os significance assumed for this case is
`\alpha=0.05`

The statistic to check the hypothesis is given by:

`\chi^2 =\sum_(i=1)^n ((O_i -E_i)^2)/(E_i)`

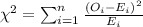
The table given represent the observed values, we just need to calculate the expected values with the following formula
`E_i = (total col * total row)/(grand total)`

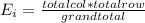
And the calculations are given by:

`E_(1) =(109*108)/(405)=29.07`

`E_(2) =(107*108)/(405)=28.53`

`E_(3) =(97*108)/(405)=25.87`

`E_(4) =(92*108)/(405)=24.53`

`E_(5) =(109*97)/(405)=26.11`

`E_(6) =(107*97)/(405)=25.63`

`E_(7) =(97*97)/(405)=23.23`

`E_(8) =(92*97)/(405)=22.03`

`E_(9) =(109*104)/(405)=27.99`

`E_(10) =(107*104)/(405)=27.48`

`E_(11) =(97*104)/(405)=24.91`

`E_(12) =(92*104)/(405)=23.62`

`E_(13) =(109*96)/(405)=25.84`

`E_(14) =(107*96)/(405)=25.36`

`E_(15) =(97*96)/(405)=22.99`

`E_(16) =(92*96)/(405)=21.81`

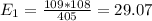
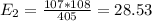
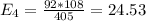
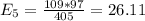
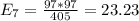
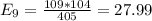
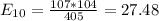
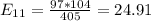
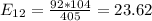
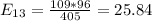
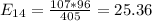
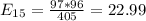
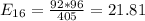
And the expected values are given by:

Amusement Parks Mexico Home Other Total

Freshman 29.07 28.53 25.87 24.53 108

Sophomore 26.11 25.63 23.23 22.03 97

Junior 27.99 27.48 24.91 23.62 104

Senior 25.84 25.36 22.99 21.81 96

Total 109 107 97 92 405

And now we can calculate the statistic:

`\chi^2 =27.356`

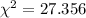
Now we can calculate the degrees of freedom for the statistic given by:

`df=(rows-1)(cols-1)=(4-1)(4-1)=9`

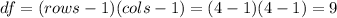
And we can calculate the p value given by:

`p_v = P(\chi^2_(9) >27.356)=0.00122`

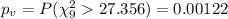
And we can find the p value using the following excel code:

"=1-CHISQ.DIST(27.356,9,TRUE)"

Since the p value is lower than the significance level assumed 0.05 we can reject the null hypothesis at 5% of significance, and we can conclude that we have association between the two variables analyzed.