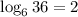The equation which is equivalent to
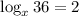 is
is
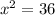 or x = 6 (
or x = 6 (
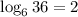 ).
).
Explanation:
Given Equation:
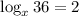
As we know, in terms of logarithmic rules, when b is raised to the power of y is equal x:
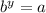
Then, the base b logarithm of x is equal to y
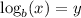
Now, use the logarithmic rule for the given equation by comparing with above equation. We get b = x, y = 2, and x = 36. Apply this in equation,
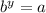
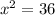
When taking out the squares on both sides, we get x = 6. Hence, the given equation can be written as