Question

`\qquad \quad \huge\color{green}\boxed{ \colorbox{black}{\colorbox{white}{Qʋestiσɳ }}}`

⧠ Topic - Damped oscillations [ grade - 11th ]

◉ A dαmped hαrmonıc oscıllαtor hαs α frequencч of 5 oscıllαtıons per second. The αmplıtude drop to hαlf of ıts vαlue for everч 10 oscıllαtıons, the tıme ıt ɯıll tαke to drop to
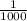
`(1)/(1000)` of the αngulαr αmplıtude ıs close to ? ☂

⧠ Given choices :

↳ 100 sec

↳ 10 sec

↳ 20 sec

↳ 50 sec

​

Answer 1

• The oscillator has frequency 5Hz

We know

`\\ \rm\rightarrowtail a=a_oe^(-\gamma t)\dots(1)`

• a is the amplitude

Now amplitude becomes half after 10oscillations .

`\\ \rm\rightarrowtail a=(a_o)/(2)`

• Frequency=5Hz
• Oscillations=10
• Time=10/5=2s

From eq(1)

`\\ \rm\rightarrowtail a=a_o e^(-\gamma t)`

• After 2s of time or 10 oscillations

`\\ \rm\rightarrowtail (a_o)/(2)=a_o e^(-\gamma t)`

`\\ \rm\rightarrowtail (1)/(2)=e^(-\gamma t)`

• Put t=2

`\\ \rm\rightarrowtail 2^(-1)=e^(-2\gamma)`

`\\ \rm\rightarrowtail 2=e^(2\gamma)`

• Remove e

`\\ \rm\rightarrowtail 2\gamma=ln2`

`\\ \rm\rightarrowtail \gamma=(ln2)/(2)\dots(2)`

Again from eq(1)

`\\ \rm\rightarrowtail a=a_o e^(-\gamma t)`

`\\ \rm\rightarrowtail (a_o)/(a)=e^(\gamma t)`

`\\ \rm\rightarrowtail ln\left((a_o)/(a)\right)=\gamma t`

• Put
  `\gamma` from eq(2)

`\\ \rm\rightarrowtail ln\left((a_o)/(a)\right)=\left((ln2)/(2)\right)t`

`\\ \rm\rightarrowtail ln1000=\left((ln2)/(2)\right)t`

`\\ \rm\rightarrowtail t=2\left((ln1000)/(ln2)\right)`

`\\ \rm\rightarrowtail t=2\left((ln10^3)/(ln2)\right)`

`\\ \rm\rightarrowtail t=2\left((3ln10)/(ln2)\right)`

`\\ \rm\rightarrowtail t=2\left((6.9077552789821)/(0.6931471805599)\right)`

`\\ \rm\rightarrowtail t=2(9.9657842846626)`

`\\ \rm\rightarrowtail t=19.9`

`\\ \rm\rightarrowtail t\approx 20s`