Question

"Select the equation of the least squares line for the data: (34.0, 1.30), (32.5, 3.25), (35.0, .65), (31.0, 6.50), (30.0, 5.85), (27.5, 8.45), (29.0, 6.50)."a. ŷ= 37.643-1.0543r b. ŷ= 1.0543x - 37.643 c. ŷ= 37.643 1.1597x d. ŷ= 41.407-1.1597x e. ŷ= -37.643 1.05433x f. None of the above

Answer 1

`y=-1.055 x +37.643`

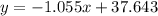
And the best option would be:

a. ŷ= 37.643-1.0543x

Explanation:

We assume that the data is this one:

x: 34.0, 32.5, 35.0, 31.0, 30.0, 27.5, 29.0

y: 1.30, 3.25, 0.65, 6.50, 5.85, 8.45, 6.50

Find the least-squares line appropriate for this data.

For this case we need to calculate the slope with the following formula:

`m=(S_(xy))/(S_(xx))`

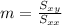
Where:

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)`

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)`

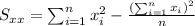
So we can find the sums like this:

`\sum_(i=1)^n x_i = 34.0+ 32.5+ 35.0+ 31.0+ 30.0+ 27.5+ 29.0 =219`

`\sum_(i=1)^n y_i =1.3+3.25+0.65+6.5+5.85+8.45+6.5=32.5`

`\sum_(i=1)^n x^2_i = 34.0^2+ 32.5^2+ 35.0^2+ 31.0^2+ 30.0^2+ 27.5^2+ 29.0^2 =6895.5`

`\sum_(i=1)^n y^2_i =1.3^2+3.25^2+0.65^2+6.5^2+5.85^2+8.45^2+6.5^2=202.8`

`\sum_(i=1)^n x_i y_i =34*1.3 + 32.5*3.25+ 35*0.65+ 31*6.5+30*5.585 +27.5*8.45 +29*6.5=970.45`

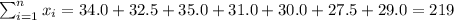
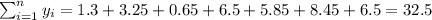
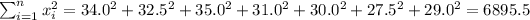
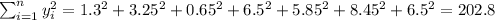
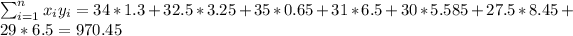
With these we can find the sums:

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)=6895.5-(219^2)/(7)=43.929`

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)=970.45-(219*32.5)/(7)=-46.336`

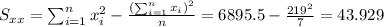
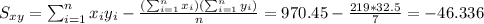
And the slope would be:

`m=-(46.336)/(43.929)=-1.055`

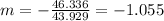
Nowe we can find the means for x and y like this:

`\bar x= (\sum x_i)/(n)=(219)/(7)=31.286`

`\bar y= (\sum y_i)/(n)=(32.5)/(7)=4.643`

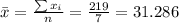
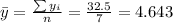
And we can find the intercept using this:

`b=\bar y -m \bar x=4.643-(-1.055*31.286)=37.643`

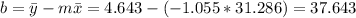
So the line would be given by:

`y=-1.055 x +37.643`

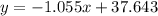
And the best option would be:

a. ŷ= 37.643-1.0543x