Answer:
112
Explanation:
Let A be a subset of S that satisfies such condition.
If 3∈A, then the other three elements of A must be chosen from the set B={1,2,5,6,7,8,9,10} (because 3 cannot be chosen again and 4 can't be alongside 3). B has eight elements, then there are
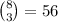 ways to select the remaining elements of A (the binomial coefficient counts this). The remaining elements determine A uniquely, then there are 56 subsets A.
ways to select the remaining elements of A (the binomial coefficient counts this). The remaining elements determine A uniquely, then there are 56 subsets A.
If 4∉A, we have to choose the remaining elements of A from the set B={1,2,5,6,7,8,9,10}. B has eight elements, then there are
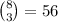 ways to select the remaining elements of A. Thus, there are 56 choices for A.
ways to select the remaining elements of A. Thus, there are 56 choices for A.
By the sum rule, the total number of subsets is 56+56=112