Question

In the workplace, racial discrimination is a very serious issue. Consider a company in which 20% of the employees are African-American. At the end of the year, promotions are awarded to a group of employees. Out of the 40 promotions awarded, five are African-American. Given that the awarding follows the binomial distribution, B(40,.2).

Answer 1

a) It is expected that 8 African-Americans get promotions.

b) There is a 8.6% probability that 5 African-Americans get promotions.

c) There is a 16.2% probability that at five or less African-Americans get promotions.

d) The company may be accused of racial discrimination because the ammount of promotions given to African-Americans is much less than expected if there were no discrimination. The expected value, if there is no discrimination, of having more than 5 promotions for African American employees is 84%.

Step-by-step explanation:

The question is incomplete.

Complete question:

In the workplace, racial discrimination is a very serious issue. Consider a company in which 20% of the employees are African-American. At the end of the year, promotions are awarded to a group of employees. Out of the 40 promotions awarded, five are African-American. Given that the awarding follows the binomial distribution, B(40,.2).

a) How many African-Americans would you expect to get promotions?

b) What is the probability that five African-Americans receive promotions?

c) What is the probability that five or fewer African-Americans receive promotions?

d) Do you think the company is suspect of racial discrimination? Explain your thinking.

a) As this situation can be modeled by a binomial distribution B(40,0.2), the expected number of African-Americans that get promotions can be calculated as the expected value of the binomial distribution:

`X\sim B(40,0.2)\\\\E(X)=np=40*0.2=8`

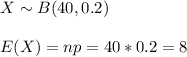
It is expected that 8 African-Americans get promotions.

b) Accordingly to the binomial distribution, we have:

`P(X=5)=(40!)/(5!35!)*(0.2)^5*(0.8)^(35)=658008*0.00032*0.0004= 0.086`

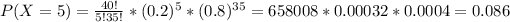
There is a 8.6% probability that 5 African-Americans get promotions.

c) We have to calculate the probabilities for X=0,1,2,3,4 and 5.

`P(X\leq5)=P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5)\\\\\\P(X=0)=(40!)/(0!40!)*0.2^0*0.8^(40)=1*1*0.00013=0\\\\P(X=1)=(40!)/(1!39!)*0.2^1*0.8^(39)=40*0.2*0.00017=0.001\\\\P(X=2)=(40!)/(2!38!)*0.2^2*0.8^(38)=780*0.04*0.00021=0.007\\\\P(X=3)=(40!)/(3!37!)*0.2^3*0.8^(37)=9880*0.008*0.00026=0.021\\\\P(X=4)=(40!)/(4!36!)*0.2^4*0.8^(36)=91390*0.0016*0.00032=0.047\\\\P(X=5)=(40!)/(5!35!)*0.2^5*0.8^(35)=658008*0.00032*0.00041=0.086`

`P(X\leq5)=P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5)\\\\P(X\leq5)=0+0.001+0.007+0.021+0.047+0.086=0.162`

There is a 16.2% probability that at five or less African-Americans get promotions.

d) The company may be accused of racial discrimination because the ammount of promotions given to African-Americans is much less than expected if there were no discrimination. The expected value, if there is no discrimination, of having more than 5 promotions for African American employees is 84%.