Answer: c)[50,60]
Explanation:
The Empirical rule says that , About 68% of the population lies with the one standard deviation from the mean (For normally distribution).
We are given that , The heights of students in a class are normally distributed with mean 55 inches and standard deviation 5 inches.
Then by Empirical rule, about 68% of the heights of students lies between one standard deviation from mean.
i.e. about 68% of the heights of students lies between
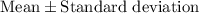
i.e. about 68% of the heights of students lies between
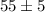
Here,

i.e. The required interval that contains the middle 68% of the heights. = [50,60]
Hence, the correct answer is c) (50,60)