Question

Please help I need to finish my winter packet and no one is answering my questions

Answer 1

`\sqrt[7]{x^(4)}`

`(x^{(1)/(7)})^(4)`

`(\sqrt[7]{x})^(4)`

Explanation:

we have

`x^{(4)/(7)}`

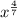
Remember the properties

`\sqrt[n]{a^(m)}=a^{(m)/(n)}`

`(a^m)^(n)=a^(m*n)`

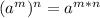
so

Verify each case

Part 1) we have

`\sqrt[4]{x^(7)}`

we know that

`\sqrt[4]{x^(7)}=x^{(7)/(4)}`

Compare with the given expression

`x^{(7)/(4)} \\eq x^{(4)/(7)}`

Part 2) we have

`\sqrt[7]{x^(4)}`

we know that

`\sqrt[7]{x^(4)}=x^{(4)/(7)}`

Compare with the given expression

`x^{(4)/(7)} = x^{(4)/(7)}`

therefore

Is equivalent to the given expression

Part 3) we have

`(x^{(1)/(7)})^(4)`

we know that

`(x^{(1)/(7)})^(4)=x^{(4)/(7)}`

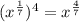
Compare with the given expression

`x^{(4)/(7)} = x^{(4)/(7)}`

therefore

Is equivalent to the given expression

Part 4) we have

`(x^{(1)/(4)})^(7)`

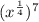
we know that

`(x^{(1)/(4)})^(7)=x^{(7)/(4)}`

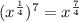
Compare with the given expression

`x^{(7)/(4)} \\eq x^{(4)/(7)}`

Part 5) we have

`(\sqrt[4]{x})^(7)`

we know that

`(\sqrt[4]{x})^(7)=(x^{(1)/(4)})^(7)=x^{(7)/(4)}`

Compare with the given expression

`x^{(7)/(4)} \\eq x^{(4)/(7)}`

Part 6) we have

`(\sqrt[7]{x})^(4)`

we know that

`(\sqrt[7]{x})^(4)=(x^{(1)/(7)})^(4)=x^{(4)/(7)}`

Compare with the given expression

`x^{(4)/(7)} = x^{(4)/(7)}`

therefore

Is equivalent to the given expression