Question

3 cards are drawn from a standard deck without replacement. What is the probability that at least one of the cards drawn is a red card?

Answer 1

Answer:
`(15)/(17)`

Explanation:

Total number of cards in a deck = 52

Number of red cards = 26

Number of cards not red =

Number of ways to draw not red cards =
`^(26)C_3`

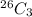
Total ways to draw 3 cards =
`^(52)C_3`

The probability that none of three cards are red =
`(^(26)C_3)/(^(52)C_3)`

`=((26!)/(3!(26-3)!))/((52!)/(3!(52-3)!))` [∵
`^nC_r=(n!)/(r!(n-r)!)`]

`=((26*25*24*23!)/((23)!))/((52*51*50*49!)/(3!(49)!))=(2)/(17)`

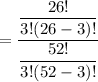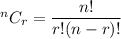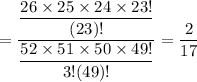
Now , the probability that at least one of the cards drawn is a red card = 1- Probability that none cards are red

`=1-(2)/(17)=(17-2)/(17)=(15)/(17)`

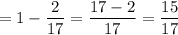
Hence, the required probability =
`(15)/(17)`