Answer:
The imaginary part is 0
Explanation:
The number given is:

First, we can expand this power using the binomial theorem:

After that, we can apply De Moivre's theorem to expand each summand:
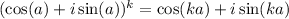
The final step is to find the common factor of i in the last expansion. Now:

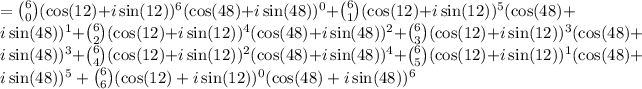

The last part is to multiply these factors and extract the imaginary part. This computation gives:
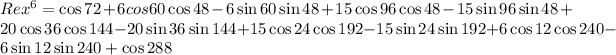

(It is not necessary to do a lengthy computation: the summands of the imaginary part are the products sin(a)cos(b) and cos(a)sin(b) as they involve exactly one i factor)
A calculator simplifies the imaginary part Im(x⁶) to 0