Question

This activity will help you meet these educational goals:

You will create a function to model a fireworks show and examine the attributes of the function.

You’re in charge of planning a fireworks show. The company you hire proposes using fireworks called mortar fireworks. These fireworks are placed in a tube that sits on the ground or a flat surface and are shot from the tube with an initial velocity that propels them into the sky.

Mortar fireworks have two fuses that are lit at the same time. The first fuse burns fastest and causes the initial force that launches the firework into the sky. The second fuse takes longer to burn. When the second fuse reaches the middle of the firework, the firework explodes and we see the light show in the sky. This second fuse does not add any extra propulsion to the firework while it’s in the air.

You plan to have the company light the fireworks from the ground. Based on information provided by the company, you’ve determined that the fireworks will have an initial velocity of 192 feet/second.

The formula for the vertical motion of an object is h = -16t2 + v0t + h0, where h is the height of the object, h0 is the initial, or starting, height, v0 is the initial velocity, and t is the time in seconds.

Part A

Create a function to model the height of a firework when shot in the air. Explain whether the function will have a maximum or a minimum value.


Part B
Using the equation representing the height of the firework (h = -16t2 + v0t + h0), algebraically determine the extreme value of f(t) by completing the square and finding the vertex. Interpret what the value represents in this situation.

Answer 1

A

`h = -16t^2 + 192t`

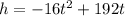
B

Vertex=(6,576)

Explanation:

The problem gives us the following data:

`v_o=192\ ft/s,\ h_o=0`

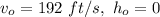
A.

Thus the function is

`h = -16t^2 + 192t`

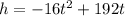
The graph of h has the shape of an inverted parabola. Recall if the coefficient of the quadratic term is negative, the parabola is concave down, so it has a maximum value.

Part B

Let's take the function of h

`h = -16t^2 + 192t`

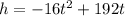
Factoring by -16

`\displaystyle h = -16(t^2 - 12t)`

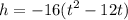
Completing squares

`\displaystyle h = -16(t^2 - 12t+36-36)`

`\displaystyle h = -16(t^2 - 12t+36)+576`

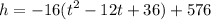
Factoring

`\displaystyle h = -16(t-6)^2+576`

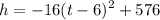
Rearranging

`\displaystyle h -576= -16(t-6)^2`

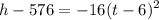
We can get the coordinates of the vertex from this standard form of the parabola.

Vertex=(6,576)

The maximum value means that at t=6 seconds, the firework will be 576 feet high and then it will start falling back to the ground.