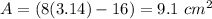Question

Semicircles

whose centers A
are the midpoints .
of the sides of
square ABCD are .
drawn. If the
measure of each
side of the square
is 4 cm, what is the area, nearest to
the tenth of a sq cm, of the shaded
portion of the figure?​

Answer 1

The area of the shaded portion of the figure is
`9.1\ cm^2`

Explanation:

see the attached figure to better understand the problem

we know that

The shaded area is equal to the area of the square less the area not shaded.

There are 4 "not shaded" regions.

step 1

Find the area of square ABCD

The area of square is equal to

`A=b^2`

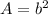
where

b is the length side of the square

we have

`b=4\ cm`

substitute

`A=4^2=16\ cm^2`

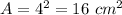
step 2

We can find the area of 2 "not shaded" regions by calculating the area of the square less two semi-circles (one circle):

The area of circle is equal to

`A=\pi r^(2)`

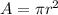
The diameter of the circle is equal to the length side of the square

so

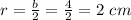`r=(b)/(2)=(4)/(2)=2\ cm` ---> radius is half the diameter

substitute

`A=\pi (2)^(2)`

`A=4\pi\ cm^2`

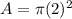
Therefore, the area of 2 "not-shaded" regions is:

`A=(16-4\pi) \ cm^2`

and the area of 4 "not-shaded" regions is:

`A=2(16-4\pi)=(32-8\pi)\ cm^2`

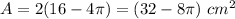
step 3

Find the area of the shaded region

Remember that the area of the shaded region is the area of the square less 4 "not shaded" regions:

so

`A=16-(32-8\pi)=(8\pi-16)\ cm^2`

---> exact value

assume

`\pi =3.14`

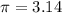
substitute

`A=(8(3.14)-16)=9.1\ cm^2`