Question

The number of rescue calls received by a rescue squad in a city follows a Poisson distribution with an average of 2.83 rescues every eight hours. What is the probability that the squad will have at most 2 calls in an hour? Round answer to 4 decimal places.

Answer 1

There is a 99.44% probability that the squad will have at most 2 calls in an hour.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given time interval.

In this problem, we have that:

2.83 rescues every eight hours.

What is the probability that the squad will have at most 2 calls in an hour?

This is

`P = P(X = 0) + P(X = 1) + P(X = 2)`

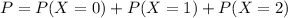
We have 2.83 rescues every 8 hours. So for an hour, we have
`\mu = (2.83)/(8) = 0.354`

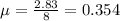
So

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-0.354)*(0.354)^(0))/((0)!) = 0.7019`

`P(X = 1) = (e^(-0.354)*(0.354)^(1))/((1)!) = 0.2485`

`P(X = 2) = (e^(-0.354)*(0.354)^(2))/((2)!) = 0.0440`

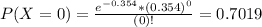
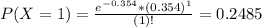
So

`P = P(X = 0) + P(X = 1) + P(X = 2) = 0.7019 + 0.2485 + 0.0440 = 0.9944`

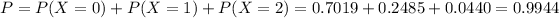
There is a 99.44% probability that the squad will have at most 2 calls in an hour.