Question

The maximum force a pilot can stand is about seven times his weight. What is the minimum radius of curvature that a jet plane's pilot, pulling out of a vertical dive, can tolerate at a speed of 250 m/s?

Answer 1

Radius of curvature of the path is 1063 meters

Step-by-step explanation:

It is given that,

Force acting on the pilot is about seven times of his weight. Speed with which pilot moves, v = 250 m/s.

As per Newton's second law of motion, the net force acting on the pilot at the bottom is given by :

`N-mg=(mv^2)/(r)`

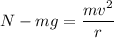
Where

N is the normal force

r is the radius of curvature

According to given condition,

`7mg-mg=(mv^2)/(r)`

`6mg=(mv^2)/(r)`

`r=(mv^2)/(6mg)`

`r=(mv^2)/(6mg)`

`r=(v^2)/(6g)`

`r=((250)^2)/(6* 9.8)`

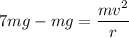
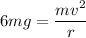
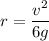
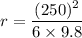
r = 1062.92 meters

or

r = 1063 meters

So, the radius of curvature of the path is 1063 meters. Hence, this is the required solution.