Answer:
The variance of the data is 29966.3.
Explanation:
The given data set is
175, 349, 234, 512, 638, 549, 500, 611
We need to find the variance to the nearest hundredth decimal place.
Mean of the data
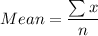
where, n is number of observation.
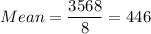
The mean of the data is 446.
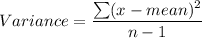
![Variance=((175-446)^2+(349-446)^2+(234-446)^2+(512-446)^2+(638-446)^2+(549-446)^2+(500-446)^2+(611-446)^2)/(8-1)]()
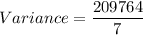
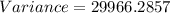
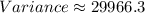
Therefore, the variance of the data is 29966.3.