Question

A laser beam of wavelength λ=632.8 nm shines at normal incidence on the reflective side of a compact disc. The tracks of tiny pits in which information is coded onto the CD are 1.60 μm apart.For what nonzero angles of reflection (measured from the normal) will the intensity of light be maximum? Express your answer numerically. If there is more than one answer, enter each answer separated by a comma.

Answer 1

To solve this problem we will apply the concepts given by the principles of superposition, specifically those described by Bragg's law in constructive interference.

Mathematically this relationship is given as

`dsin\theta = n\lambda`

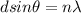
Where,

d = Distance between slits

`\lambda` = Wavelength

n = Any integer which represent the number of repetition of the spectrum

`\theta = sin^(-1) ((n\lambda)/(d))`

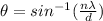
Calculating the value for n, we have

n = 1

`\theta_1 = sin^(-1) ((\lambda)/(d))\\\theta_1 = sin^(-1) ((632.8*10^(-9))/(1.6*10^(-6)))\\\theta_1 = 23.3\°`

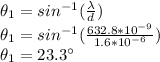
n=2

`\theta_2 = sin^(-1) ((2\lambda)/(d))\\\theta_2 = sin^(-1) (2(632.8*10^(-9))/(1.6*10^(-6)))\\\theta_2 = 52.28\°`

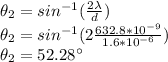
n =3

`\theta_2 = sin^(-1) ((2\lambda)/(d))\\\theta_2 = sin^(-1) (3(632.8*10^(-9))/(1.6*10^(-6)))\\\theta_2 = \text{not possible}`

Therefore the intensity of light be maximum for angles 23.3° and 52.28°