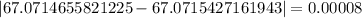Question

Consider the integral Integral from 0 to 1 e Superscript 6 x Baseline dx with nequals 25 . a. Find the trapezoid rule approximations to the integral using n and 2n subintervals. b. Find the​ Simpson's rule approximation to the integral using 2n subintervals. c. Compute the absolute errors in the trapezoid rule and​ Simpson's rule with 2n subintervals.

Answer 1

a.

With n = 25,
`\int_(0)^(1)e^(6 x)\ dx \approx 67.3930999748549`

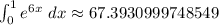
With n = 50,
`\int_(0)^(1)e^(6 x)\ dx \approx 67.1519320308594`

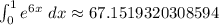
b.
`\int_(0)^(1)e^(6 x)\ dx \approx 67.0715427161943`

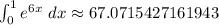
c.

The absolute error in the trapezoid rule is 0.08047

The absolute error in the Simpson's rule is 0.00008

Explanation:

a. To approximate the integral
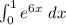`\int_(0)^(1)e^(6 x)\ dx` using n = 25 with the trapezoid rule you must:

The trapezoidal rule states that

`\int_(a)^(b)f(x)dx\approx\frac{\Delta{x}}{2}\left(f(x_0)+2f(x_1)+2f(x_2)+...+2f(x_(n-1))+f(x_n)\right)`

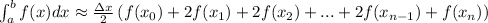
where
`\Delta{x}=(b-a)/(n)`

We have that a = 0, b = 1, n = 25.

Therefore,

`\Delta{x}=(1-0)/(25)=(1)/(25)`

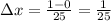
We need to divide the interval [0,1] into n = 25 sub-intervals of length
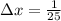`\Delta{x}=(1)/(25)`, with the following endpoints:

`a=0, (1)/(25), (2)/(25),...,(23)/(25), (24)/(25), 1=b`

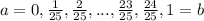
Now, we just evaluate the function at these endpoints:

`f\left(x_(0)\right)=f(a)=f\left(0\right)=1=1`

`2f\left(x_(1)\right)=2f\left((1)/(25)\right)=2 e^{(6)/(25)}=2.54249830064281`

`2f\left(x_(2)\right)=2f\left((2)/(25)\right)=2 e^{(12)/(25)}=3.23214880438579`

...

`2f\left(x_(24)\right)=2f\left((24)/(25)\right)=2 e^{(144)/(25)}=634.696657835701`

`f\left(x_(25)\right)=f(b)=f\left(1\right)=e^(6)=403.428793492735`

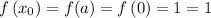
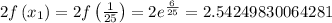
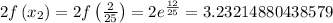
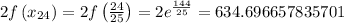
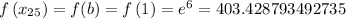
Applying the trapezoid rule formula we get

`\int_(0)^(1)e^(6 x)\ dx \approx (1)/(50)(1+2.54249830064281+3.23214880438579+...+634.696657835701+403.428793492735)\approx 67.3930999748549`

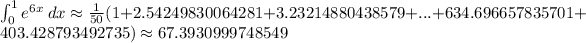
• To approximate the integral
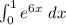  `\int_(0)^(1)e^(6 x)\ dx` using n = 50 with the trapezoid rule you must:

We have that a = 0, b = 1, n = 50.

Therefore,

`\Delta{x}=(1-0)/(50)=(1)/(50)`

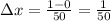
We need to divide the interval [0,1] into n = 50 sub-intervals of length
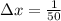`\Delta{x}=(1)/(50)`, with the following endpoints:

`a=0, (1)/(50), (1)/(25),...,(24)/(25), (49)/(50), 1=b`

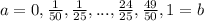
Now, we just evaluate the function at these endpoints:

`f\left(x_(0)\right)=f(a)=f\left(0\right)=1=1`

`2f\left(x_(1)\right)=2f\left((1)/(50)\right)=2 e^{(3)/(25)}=2.25499370315875`

`2f\left(x_(2)\right)=2f\left((1)/(25)\right)=2 e^{(6)/(25)}=2.54249830064281`

...

`2f\left(x_(49)\right)=2f\left((49)/(50)\right)=2 e^{(147)/(25)}=715.618483417705`

`f\left(x_(50)\right)=f(b)=f\left(1\right)=e^(6)=403.428793492735`

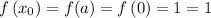
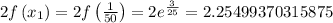
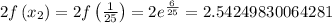
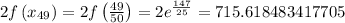
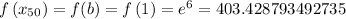
Applying the trapezoid rule formula we get

`\int_(0)^(1)e^(6 x)\ dx \approx (1)/(100)(1+2.25499370315875+2.54249830064281+...+715.618483417705+403.428793492735) \approx 67.1519320308594`

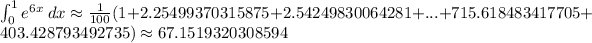
b. To approximate the integral
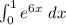`\int_(0)^(1)e^(6 x)\ dx` using 2n with the Simpson's rule you must:

The Simpson's rule states that

`\int_(a)^(b)f(x)dx\approx \\\frac{\Delta{x}}{3}\left(f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+2f(x_4)+...+2f(x_(n-2))+4f(x_(n-1))+f(x_n)\right)`

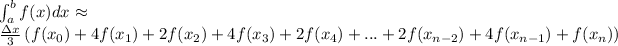
where
`\Delta{x}=(b-a)/(n)`

We have that a = 0, b = 1, n = 50

Therefore,

`\Delta{x}=(1-0)/(50)=(1)/(50)`

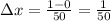
We need to divide the interval [0,1] into n = 50 sub-intervals of length
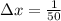`\Delta{x}=(1)/(50)`, with the following endpoints:

`a=0, (1)/(50), (1)/(25),...,(24)/(25), (49)/(50), 1=b`

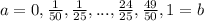
Now, we just evaluate the function at these endpoints:

`f\left(x_(0)\right)=f(a)=f\left(0\right)=1=1`

`4f\left(x_(1)\right)=4f\left((1)/(50)\right)=4 e^{(3)/(25)}=4.5099874063175`

`2f\left(x_(2)\right)=2f\left((1)/(25)\right)=2 e^{(6)/(25)}=2.54249830064281`

...

`4f\left(x_(49)\right)=4f\left((49)/(50)\right)=4 e^{(147)/(25)}=1431.23696683541`

`f\left(x_(50)\right)=f(b)=f\left(1\right)=e^(6)=403.428793492735`

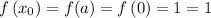
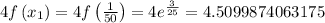
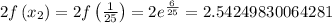
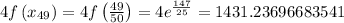
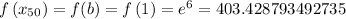
Applying the Simpson's rule formula we get

`\int_(0)^(1)e^(6 x)\ dx \approx (1)/(150)(1+4.5099874063175+2.54249830064281+...+1431.23696683541+403.428793492735) \approx 67.0715427161943`

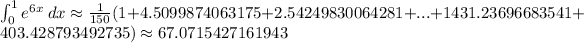
c. If B is our estimate of some quantity having an actual value of A, then the absolute error is given by
`|A-B|`

The absolute error in the trapezoid rule is

The calculated value is

`\int _0^1e^(6\:x)\:dx=(e^6-1)/(6) \approx 67.0714655821225`

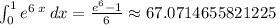
and our estimate is 67.1519320308594

Thus, the absolute error is given by

`|67.0714655821225-67.1519320308594|=0.08047`

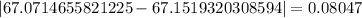
The absolute error in the Simpson's rule is

`|67.0714655821225-67.0715427161943|=0.00008`