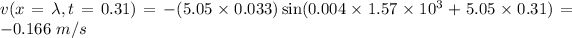Question

A water wave traveling in a straight line on a lake is described by the equation

y(x,t) = (3.30 cm) cos(0.400 cm?1x + 5.05 s?1t)

where y is the displacement perpendicular to the undisturbed surface of the lake.

(a) How much time does it take for one complete wave pattern to go past a fisherman in a boat at anchor?

What horizontal distance does the wave crest travel in that time?

b) What are the wave number and the number of waves per second that pass the fisherman?

(c) How fast does a wave crest travel past the fisherman?

What is the maximum speed of his cork floater as the wave causes it to bob up and down?

Answer 1

A) The wave equation is given as

`y(x,t) = A\cos(kx + \omega t)=(3.3* 10^(-2))\cos(0.004x + 5.05t)\\`

According to the above equation, k = 0.004 and ω = 5.05.

Using the following identities, we can find the period of the wave.

`\omega = 2\pi f\\ f = 1/ T`

T = 1.25 s.

For the horizontal distance travelled by one period of time, x = λ.

`\lambda = 2\pi / k = 2\pi / 0.004 = 1.57* 10^3~m`

`y(x = \lambda,t = T) = 0.033\cos(0.004*1.57*\10^3 + 5.05*1.25) = 0.033~m`

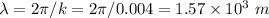
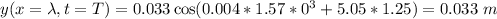
B) The wave number, k = 0.004 . The number of waves per second is the frequency, so f = 0.8.

C) The propagation speed of the wave is

`v = \lambda f = 1.57* 10^3 * 0.8 = 1.256* 10^3~m/s`

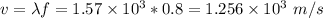
The velocity of the wave is the derivative of the position function.

`v(x,t) = (dy(x,t))/(dt) = -(5.05* 0.033)\sin(0.004x + 5.05t)`

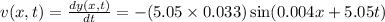
The maximum velocity is when the derivative of the velocity function is equal to zero.

`(dv_y(x,t))/(dt) = -(5.05)^2(0.033)\cos(0.004*1.57* 10^3 + 5.05t) = 0`

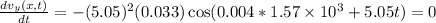
In order this to be zero, cosine term must be equal to zero.

`0.004*1.57* 10^3 + 5.05t = 5\pi /2\\t = 0.31~s`

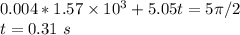
The reason that cosine term is set to be 5π/2 is that time cannot be zero. For π/2 and 3π/2, t<0.

`v(x=\lambda, t = 0.31) = -(5.05*0.033)\sin(0.004* 1.57* 10^3 + 5.05* 0.31) = -0.166~m/s`