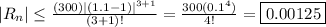Hi there!
a.
Recall the equation for a Taylor expansion:
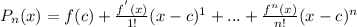
**Where the numerator of the coefficient is the derivative evaluated at the point, and c = where the polynomial is centered.
We can plug in the given values to solve.
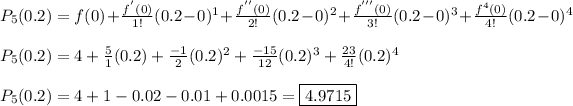
b.
At x = 0, f(x³) = f(x) because 0³ = 0, so we can simply take the derivative of the polynomial to find g'(x).
Differentiate the following.
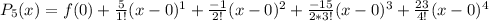
Simplify:
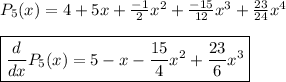
c.
The third degree will include n = 0, 1, and 2. Also, c = 1 in this instance, so using the format above:
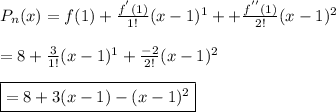
d.
Using the equation for the Lagrange error bound:

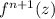 is the maximum value of the fourth derivative (since we are doing a third-degree polynomial), which is given to us in the problem.
is the maximum value of the fourth derivative (since we are doing a third-degree polynomial), which is given to us in the problem.
We also know that:
n = 3
c = 1
x = 1.1
We can plug in the values: