Question

What is the common difference of an AP which has its first term as 100 and the sum of its first 6 terms = 5 times the sum of its next six terms Pick one of the choices 1. 10 2. -10 3. 12 4. 15

Answer 1

The common difference of given AP is Option 2) -10.

Explanation:

We are given the following information in the question:

First term of AP, a = 100

The sum of its first 6 terms = 5(the sum of its next six terms)

We have to find the common difference of AP.

The sum of n terms of AP is given by:

`S_n = (n)/(2)\big(2a + (n-1)d\big)`

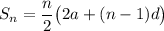
where a is the first term and d is the common difference.

Thus, we can write:

`S_6 = 5 (S_(12)-S_6)\\(6)/(2)\big(200 + (6-1)d\big) = 5\bigg((12)/(2)\big(200 + (12-1)d\big)-(6)/(2)\big(200 + (6-1)d\big)\bigg)\\\\600 + 15d =5(1200+66d-600-15d)\\600+15d=3000+255d\\2400 = -240d\\d = -10`

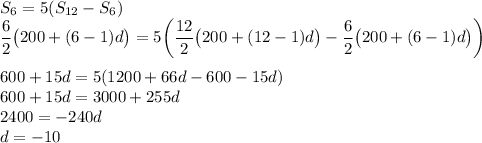
Thus, the common difference of given AP is -10.