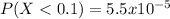Question

Tanya enters a raffle at the local fair, and is wondering what her chances of winning are.

If her probability of winning can be modeled by a beta distribution with α = 5 and β = 2, what is the probability that she has at most a 10% chance of winning?

Answer 1

`P(X<0.1)= 5.5x10^(-5)`

Explanation:

Previous concepts

Beta distribution is defined as "a continuous density function defined on the interval [0, 1] and present two parameters positive, denoted by α and β, both parameters control the shape. "

The probability function for the beta distribution is given by:

`P(X)= (x^(\alpha-1) (1-x)^(\beta -1))/(B(\alpha,\beta))`

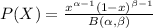
Where B represent the beta function defined as:

`B(\alpha,\beta)= (\Gamma(\alpha)\Gamma(\beta))/(\Gamma(\alpha+\beta))`

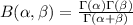
Solution to the problem

For our case our random variable is given by:

`X \sim \beta (\alpha=5, \beta =2)`

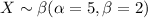
We can use the following R code to plot the distribution for this case:

> x=seq(0,1,0.01)

> plot(x,dbeta(x,5,2),main = "Beta distribution a=5, b=2",ylab = "Probability")

And we got as the result the figure attached.

And for this case we want this probability, since we want the probability that she has at most 10% or 0.1 change of winning:

`P(X<0.1)`

And we can find this probability with the following R code:

> pbeta(0.1,5,2)

[1] 5.5e-05

And we got then this :
`P(X<0.1)= 5.5x10^(-5)`