Answer:
50 Minutes.
Explanation:
The function c approximates the total number of calls made after m minutes since the start of the phone tree.
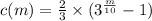
We need to find the number of minutes after which the total number of calls will 363.
Substitute c(m)=363 in the given function.
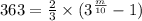
Multiply 3/2 both sides.
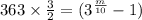
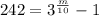
Add 1 on both sides.
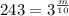
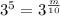
On comparing both sides we get
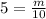
Multiply both sides by 10.
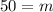
Therefore, the total number of calls will 363 after 50 minutes since the start of the phone tree.