Question

The Golden Years Senior Citizen Center uses a phone tree to announce when the center will be closed for poor weather. When each person receives a phone call, that person has a list of three more people to call. The function c approximates the total number of calls made after m minutes since the start of the phone tree. c(m) = 3/2 * (3 ^ (m/10) - 1) Approximately how many minutes will it take for the number of calls to reach 363?

Answer 1

50 minutes

Explanation:

Answer 2

50 Minutes.

Explanation:

The function c approximates the total number of calls made after m minutes since the start of the phone tree.

`c(m)=(2)/(3)* (3^{(m)/(10)}-1)`

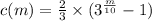
We need to find the number of minutes after which the total number of calls will 363.

Substitute c(m)=363 in the given function.

`363=(2)/(3)* (3^{(m)/(10)}-1)`

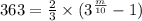
Multiply 3/2 both sides.

`363* (3)/(2)=(3^{(m)/(10)}-1)`

`242=3^{(m)/(10)}-1`

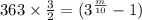
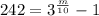
Add 1 on both sides.

`243=3^{(m)/(10)}`

`3^5=3^{(m)/(10)}`

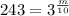
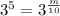
On comparing both sides we get

`5=(m)/(10)`

Multiply both sides by 10.

`50=m`

Therefore, the total number of calls will 363 after 50 minutes since the start of the phone tree.