Answer:
the position equation of the projectile are
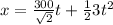
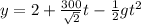
in x and y direction
Explanation:
let the mass of the projectile be m, initial velocity be u
the wind applies a force of 3 newton in east direction.
therefore acceleration due to the force in east direction =
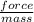
=
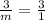
acceleration due to gravity is in south direction = g
let east be x direction and north be y direction.
therefore acceleration in x direction = 3
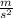 and in y direction = -g
and in y direction = -g
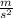
writing equation of motion in x and y direction:
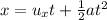

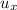 = ucos45 =
= ucos45 =
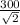
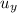 = usin45=
= usin45=
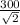
therefore
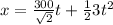
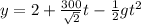
here 2 is added as the projectile already 2 meter above the ground