Question

You want to test your newly created Web site, so you have 250 people access it from random locations at random times. Of the people accessing the site, 75 of them experience computer crashes. You want to estimate the proportion of crashes within a margin of error of 4% at a 95% confidence interval. What sample size do you need?

Answer 1

Answer: 505

Explanation:

The formula to find the sample size n , if the prior estimate of the population proportion (p) is known:

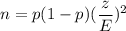`n= p(1-p)((z)/(E))^2` , where E= margin of error and z = Critical z-value.

Let p be the population proportion of crashes.

Prior sample size = 250

No. of people experience computer crashes = 75

Prior proportion of crashes
`p=(75)/(250)=0.3`

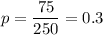
E= 0.04

From z-table , the z-value corresponding to 95% confidence interval = z=1.96

Required sample size will be :

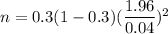`n=0.3(1-0.3)((1.96)/(0.04))^2` (Substitute all the values in the above formula)

`n= (0.21)(49)^2= 0.21*2401`

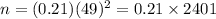
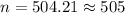`n= 504.21\approx505` (Rounded to the next integer.)

∴ Required sample size = 505