Answer:
The system cannot be solved by a unique cost for each soldier
Explanation:
The correct question is
The denarius was a unit of currency in ancient Rome. Suppose it costs the Roman government 10 denarius per day to support 3 legionaries and 3 archers. It only costs 3 denarius per day to support one legionary and one archer. Use a system of linear equations in two variables.
Can we solve for a unique cost for each soldier?
Let
x-------> the cost of a legionary per day
y-------> the cost of an archer per day
we know that

isolate the variable y
subtract 3x both sides
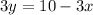
Divide by 3 both sides
 ------> equation A
------> equation A
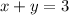
isolate the variable y
subtract x both sides
 ------> equation B
------> equation B
Remember , If two lines are parallel, then their slopes are equal
In this problem Line A and Line B are parallel lines, because their slopes are equal.
we know that that the solution of the system of equations is the intersection point both graphs
If the lines are parallel, then the lines don't intersect
see the attached figure to better understand the problem
therefore
The system has no solutions (Is a inconsistent system)