
Given :-
- Here, we have given one isosceles trapezoid that is MATH
- In the given trapezoid, MA and HT are the bases and LV is a median
- The length of MA = 3y - 2 , HT = 2y + 4 and LV = 8.5
Part 1 :-
Part 2 :-
Here, we have to
We know that the,
Length of the median of trapezium
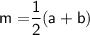
- Here, a and b are the parallel sides of the trapezium.
Subsitute the required values in the above formula :-
![\sf{ LV = }{\sf{(1)/(2)}}{\sf{ [MA + HT]}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/p5tmcwoqlgfyyw72f2yat0tfvs6pjk5j0a.png)
![\sf{ 8.5 = }{\sf{(1)/(2)}}{\sf{[ (3y - 2) + (2y + 4)]}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/m040j0h5bwgjna3o6vtochtp4wv6nhh0fh.png)
![\sf{ 8.5 = }{\sf{(1)/(2)}}{\sf{ [3y - 2 + 2y + 4]}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/n4mfzdfhhcpgsz7e9a5lkw316x6ifv3vns.png)
![\sf{ 8.5 = }{\sf{(1)/(2)}}{\sf{ [5y + 2] }}](https://img.qammunity.org/2023/formulas/mathematics/high-school/wg5hw3o7c2umzw98ne384od7u91z4f0ots.png)
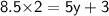
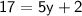
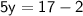
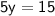
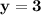
Hence, The value of y is 3
Part 3 :-
Here, we have to find the length of MA and HT
- We have, MA = 3y - 2
- HT = 2y + 4
For MA
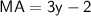
Subsitute the value of y
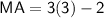
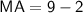
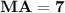
For HT
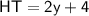
Subsitute the value of y
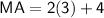

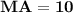
Hence, The length of MA and HT are 7 and 10 .