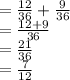Question

When rolling two fair, standard dice, what is the probability that the sum of the numbers rolled is a multiple of 3 or 4?

Answer 1

The probability that sum of numbers rolled is a multiple of 3 or 4 is:
`(7)/(12)`.

Explanation:

The sample space for two fair die (dice) is given below:

`\left[\begin{array}{ccccccc}&1&2&3&4&5&6\\1&2&3&4&5&6&7\\2&3&4&5&6&7&8\\3&4&5&6&7&8&9\\4&5&6&7&8&9&10\\5&6&7&8&9&10&11\\6&7&8&9&10&11&12\end{array}\right]`

From the above table:

Number of occurrence where sum is multiple of 3 = 12

Number of occurrence where sum is multiple of 4 = 9

Total number in the sample space = 36

probability(sum is 3) = 12/36

probability(sum is 4) = 9/36

probability(sum is 3 or 4)
`=(12)/(36) +(9)/(36) \\=(12 + 9)/(36) \\=(21)/(36)\\=(7)/(12)`