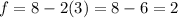Question

The local deli charges a fee, f, for delivery. On Monday, they delivered two dozen bagels, b, to an office at a total cost of 58. On Tuesday, three dozen bagels were delivered at a total cost of $11. Which system of equations could be used to find the cost of a dozen bagels?

Answer 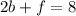1

`2b+f = 8` (1)

`3b+f=11` (2)

`b = 11-8=3`

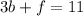`f= 8-2(3) = 8-6 =2`

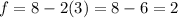
Explanation:

For this case we can put some notation

Let b= dozen bagels and f= delivery fee

And for this case we know that "On Monday, they delivered two dozen bagels, b, to an office at a total cost of $8", so then the total taling in count the delivery fee we have this:

`2b+f = 8`

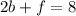
And for the other part "On Tuesday, three dozen bagels were delivered at a total cost of $11", we can write the expression like this:

`3b+f=11`

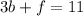
And our system of equations would be:

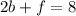`2b+f = 8` (1)

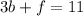`3b+f=11` (2)

If we solve for f from equation (1) we got:

`f= 8-2b`

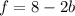
And if w replace this into equation (2) we got:

`3b+8-2b=11`

`b = 11-8=3`

And solving for f we got:

`f= 8-2(3) = 8-6 =2`