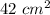Answer:
Explanation:
Area Of Triangle And Rectangle
Given a triangle of base b and height h (perpendicular to b), the area can be computed by
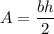
A rectangle of the same dimensions has an area of

We have a triangle of base 3 cm and a height of 4 cm. Its area is
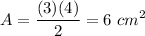
That triangle moves upward at 4 cm per second for 3 seconds. It means that the triangle 'sweeps' upwards three times its height forming a rectangle of base 3 cm and height 12 cm. The area of the swept area is
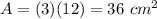
The triangle stays in the top of this rectangle, so its area is part of the total swept area:
Total swept area = 6 + 36 =