Question

The number of traffic accidents occurring on any given day in Coralville is Poisson distributed with mean 5. The probability that any such accidentinvolves an uninsured driver is 0.25, independent of all other such accidents.

Calculate the probability that on a given day in Coralville there are no trafficaccidents that involve an uninsured driver.



The answer is 0.278. Could you please explain why?

Answer 1

The answer is 0.2865

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given time interval.

In this problem, we have that:

The mean number of accidents on any given day in Coralville is 5. Of those, 25% are with an uninsured drive.

So
`\mu = 5*0.25 = 1.25`

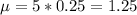
Calculate the probability that on a given day in Coralville there are no trafficaccidents that involve an uninsured driver.

This is P(X = 0). So

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-1.25)*(1.25)^(0))/((0)!) = 02865`