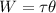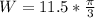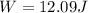To solve this problem we will use the concepts related to Torque as a function of the Force in proportion to the radius to which it is applied. In turn, we will use the concepts of energy expressed as Work, and which is described as the Torque's rate of change in proportion to angular displacement:

Where,
F = Force
r = Radius
Replacing we have that,

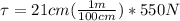
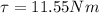
The moment of inertia is given by 2.5kg of the weight in hand by the distance squared to the joint of the body of 24 cm, therefore

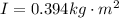
Finally, angular acceleration is a result of the expression of torque by inertia, therefore
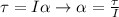

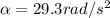
PART B)
The work done is equivalent to the torque applied by the distance traveled by 60 °° in radians
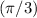 , therefore
, therefore