Question

To estimate the length of the lake, caleb starts at one end of the lake and walk 95m. He then turns a 60° angle and walks on a new path and walks 8m more then arrives at the other end of the lake. Approximately how long is the lake?

Answer 1

Length of the lake is 97.30 m

Explanation:

We have given Caleb starts at one end of the lake and walk 95 m

So
`d_1=95m`

And then he turns at an angle of 60°

So
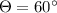`\Theta =60^(\circ)` and then again walk 8 m

So
`d_2=8m`

We have to fond the total length of the lake , that is d

Total length of the lake is given by
`d=√(d_1^2+d_2^2+2d_1d_2cos\Theta )=\sqrt{95^2+8^2+2* 95* 8* cos60^(\circ)}=97.30m`

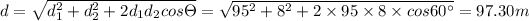
So length of the lake is 97.30 m