Average speed of slower car = 60 mph
Average speed of faster car = 70 mph
Solution:
Given that Two cars enter the Delaware turnpike at shoreline drive at 8 am, each heading for ocean city
Given that One cars average speed is 10 mph faster than the other
Let "x" be the average speed of slower car
Then x + 10 is the average speed of faster car
The faster car arrives at ocean city at 11 am, a half hour before the slower car
Time taken by faster car:
The faster car arrives at ocean city at 11 am but given that they start at 8 a.m
So time taken by faster car = 11 am - 8am = 3 hours
Time taken by slower car:
The faster car arrives at ocean city at 11 am, a half hour before the slower car
So slower car takes half an hour more than faster car
Time taken by slower car = 3 hour + half an hour =
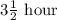
Now the distance between Delaware turnpike at shoreline drive and ocean city will be same for both cars
Let us equate the distance and find value of "x"
The distance is given by formula:
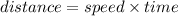
Distance covered by faster car:
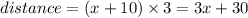
Distance covered by slower car:
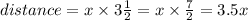
Equating both the distance,
3x + 30 = 3.5x
3x - 3.5x = -30
-0.5x = -30
x = 60
Thus average speed of slower car = 60 mph
Average speed of faster car = x + 10 = 60 + 10 = 70 mph