Question

Rewrite with only sin x and cos x.

cos 3x

A. cos x - 4 cos x sin2x
B. -sin3x + 2 sin x cos x
C. -sin2x + 2 sin x cos x
D. 2 sin2x cos x - 2 sin x cos x

Answer 1

Option A

`\cos 3 x=\cos x-4 \cos x \sin ^(2) x`

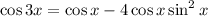
Solution:

Given that we have to rewrite with only sin x and cos x

Given is cos 3x

`cos 3x = cos(x + 2x)`

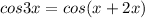
We know that,

`\cos (a+b)=\cos a \cos b-\sin a \sin b`

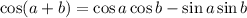
Therefore,

`\cos (x+2 x)=\cos x \cos 2 x-\sin x \sin 2 x` ---- eqn 1

We know that,

`\sin 2 x=2 \sin x \cos x`

`\cos 2 x=\cos ^(2) x-\sin ^(2) x`

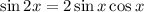
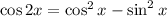
Substituting these values in eqn 1

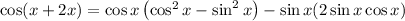`\cos (x+2 x)=\cos x\left(\cos ^(2) x-\sin ^(2) x\right)-\sin x(2 \sin x \cos x)` -------- eqn 2

We know that,

`\cos ^(2) x-\sin ^(2) x=1-2 \sin ^(2) x`

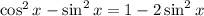
Applying this in above eqn 2, we get

`\cos (x+2 x)=\cos x\left(1-2 \sin ^(2) x\right)-\sin x(2 \sin x \cos x)`

`\begin{aligned}&\cos (x+2 x)=\cos x-2 \sin ^(2) x \cos x-2 \sin ^(2) x \cos x\\\\&\cos (x+2 x)=\cos x-4 \sin ^(2) x \cos x\end{aligned}`

`\cos (x+2 x)=\cos x-4 \cos x \sin ^(2) x`

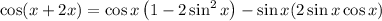
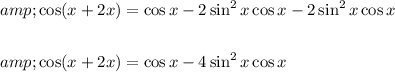
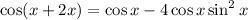
Therefore,

`\cos 3 x=\cos x-4 \cos x \sin ^(2) x`

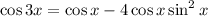
Option A is correct