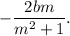Question

Two perpendicular lines have opposite y-intercepts. The equation of one of these lines is

y=mx+b. Express the x-coordinate of the intersection point of the lines in terms of m and b.


The x-coordinate is x =_____

Plz help me and fast!

Answer 1

Answer: The required x-co-ordinate of the point of intersection of two lines is
`-(2bm)/(m^2+1).`

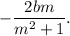
Step-by-step explanation: Given that two perpendicular lines have opposite y-intercept and the equation of one of the lines is

`y=mx+b.`

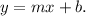
We are to express the x-coordinate of the intersection point of the lines in terms of m and b.

Let the slope and y-intercept of the other line be s and c respectively.

Since the product of the slopes of two perpendicular lines is -1 and -b is the opposite of b, so we have

`ms=-1~~~\Rightarrow s=-(1)/(m)`

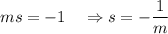
and c = -b.

That is, the equation of the other line is

`y=sx+c\\\\\Rightarrow y=-(1)/(m)-b.`

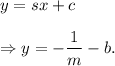
Comparing the equations of both the lines, we get

`mx+b=-(1)/(m)x-b\\\\\\\Rightarrow mx+(1)/(m)x=-2b\\\\\\\Rightarrow (m^2+1)/(m)x=-2b\\\\\\\Rightarrow x=-(2bm)/(m^2+1).`

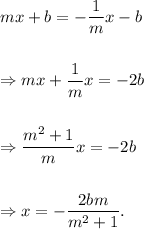
Thus, the required x-co-ordinate of the point of intersection of two lines is
`-(2bm)/(m^2+1).`